三角比のθ>90度の場合がよくわからない

質問

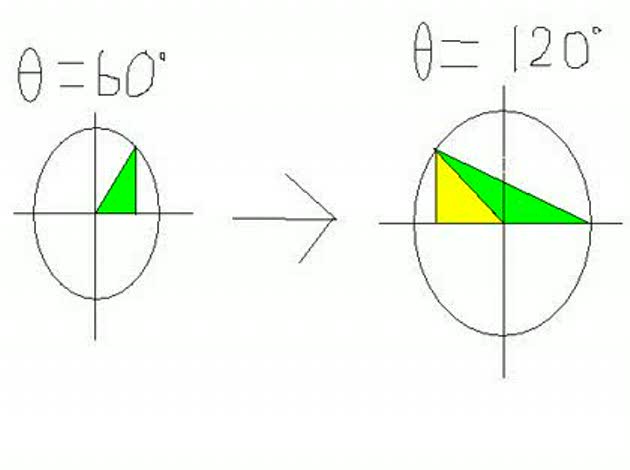
添付ファイルについて、例えば左の図でθ=60度としてsinとかcosを求める場合って緑色の三角形について考えてますよね。
ところが右の図のθ=120度とした場合のsinやcosを求めるときって、角度が１２０度の三角形について考えるのだから頂点が図の左上に引っ張られた緑色の三角形について考えるのではないのでしょうか。
どうも参考書を見てると、こういうケースの場合、頂点を移動させたところからＸ軸に垂直に線を垂らしてできた三角形、つまり黄色の三角形についてsinやcosを求めてますが、全く別の三角形のを求めてる気がするんですけど・・

そもそも黄色の三角を求めたいなら、なんで最初からθ=120ではなくθ=60で考えないのでしょうか。もしかして三角比って直角三角形の時でしか考えられないのですか。

回答No.6

arrysthmia

＞ sin360とかって、一つの角度が360度の三角形について
＞ その三角形の斜辺を何倍するとその三角形の対辺になるか
＞ ってことを考えてるってことですよね？

違います。
だから、直角三角形を考えるのは角度が鋭角の場合だけだと
最初から言っているでしょう？
角度が 90°以上だったり、マイナスだったりするものは、
三角関数であって、三角比ではなく、
したがって、直角三角形とは直接は関係がありません。
直角三角形を書こうとしてはイケナイのです。

例えば sin 120°の場合、
三角関数の性質 sin(360°-θ) = sin θ を使って
関係式 sin 120°= sin 60°を出すと、
sin 60°なら鋭角だから、三角比で考えられて、
60°の角を持つ直角三角形を書けば、値が解る。
これが、黄色の三角形です。

＞ 図の緑の三角は、左の60度の三角を120度に拡張した三角です。
＞ θ＝120で三角比を求めるってことはこの三角について考えるんですよね？

違います。
120°の角を持つ直角三角形など、書きようがありません。
右図の緑の三角形の、いったい何処に直角があるんですか？
θ = 120°の三角関数は在っても、
θ = 120°の三角比など存在しないのです。
直角三角形で考える (すなわち三角比で考える) ためには、
0 ＜ θ ＜ 90°の場合へ話をスリ換える必要があります。
そのために、三角関数の諸公式を使うのです。

回答No.5

shintaro-2

＃３です

＞でもやっぱり下半分の説明がよくわかりません！

>>しかし、cosθ=-cosθとした方が、

これが意味不明ですね。
cosθ=-cos（π－θ）の間違いです。
ごめんなさい(^^ゞ

直角三角形のsinθ,cosθについては、まさに高さ／斜辺，底辺／斜辺なので、
三角定規の
θ＝４５なら、1^2+1^2=（√2）^2で、sinθ=cosθ=１／（√２）となりますし、
θ＝30、60なら、1^2+（√3）^2＝2^2から計算できます。

θ=120,150より、θ=60,30の方が楽でしょ（覚えなくて済むし）

回答No.4

arrysthmia

←No.1 補足
不思議ですか？ θが鋭角だということは、
直角三角形が普通に書ける ということですよ。
何の不思議もない三角比の場合の話
だと思いますが。

No.1 に書いたように、直角三角形ではなく
円を使って三角関数を定義すると、
自然に sin(360°-θ) = sin θ　のような
関係が導けますから、
sin 120°= sin 60° であることがわかって、
三角関数の値 sin 120°が、
黄色の三角形の 60°に関する三角比で
考えられるようになるのです。

それにしても、120°のほうの緑の三角形は
いったい何ですか？

補足

う～んなんとなーくわかったような気がしないでもないです・・

でもすごい不思議なんですよねー。
sin360とかって、一つの角度が360度の三角形についてその三角形の斜辺を何倍するとその三角形の対辺になるかってことを考えてるってことですよね？
そもそも角度が360度の三角形なんて存在するんでしょうか。

ちなみに図の緑の三角は、左の60度の三角を120度に拡張した三角です。θ＝120で三角比を求めるってことはこの三角について考えるんですよね？

回答No.3

shintaro-2

三角比を一般の三角形に適用すると、
a^2=b^2+c^2-2bccosA　　（Aは辺ａに向かい合う角）
（b^2,c^2も同様）
ａ／sinA=ｂ／sinB=c/sinC＝２Rとなります。　（Rは半径）

θ＞９０のとき
緑色の三角形で考えるとb,cは常に１ですが、ａが１ではなくなるので、辺aの長ささえ計算できれば、cosAの数値は計算できます。

しかし、cosθ=-cosθとした方が、直角三角形でa^2+b^2=c^2が使え計算が楽です。

お礼

参考書を読み進めてやっとその式の意味がわかりました。
三角比って直角三角形以外の普通の三角形にも適用できるんですね。しかも使ってる参考書には最初の式のAは辺ａに向かい合う角という説明がなく、問題を解くときにわからなかったので、ここではっきりしてよかったです。

でもやっぱり下半分の説明がよくわかりません！

補足

げ！なんですかその式！？見たことないです！
言ってる事が難しすぎてちょっとよくわかりません・・

回答No.2

ymmasayan

>　もしかして三角比って直角三角形の時でしか考えられないのですか
その通りです。sinを例にとると高さ(符号有り)／半径(符号は常にプラス)です。
約束事ですので丸暗記して下さい。

しいて言えば長さ１の棒が回転している時横から見た高さがsinの値です。

補足

やはりそうでしたか。
でも黄色の三角のsinとかcosとか求めるだけで緑の三角のsinやcosも勝手に求まるなんてほんと不思議ですね

回答No.1

arrysthmia

その通り。
三角比は、直角三角形でしか考えられません。
角度が 90゜以上だったり、マイナスだったり
するものは、三角比ではなく、「三角関数」です。
それは、単位円上で偏角がθである点の
座標が (cosθ, sinθ) として定義され、
θが鋭角の範囲では、「三角比」と一致します。

補足

θが鋭角でも三角比と一致するんですね。不思議です。
でも、どうもやってる作業では緑の三角を求めてない気がするんです・・