正八面体に内接する球

質問

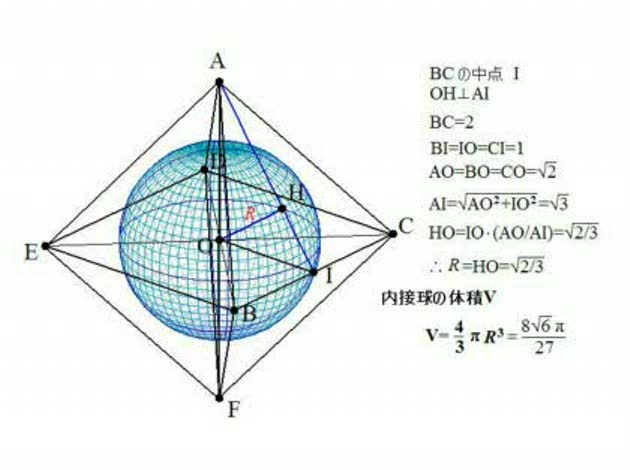
一辺の長さが２の正八面体ABCDEFがある。この正八面体に内接する球の体積を求めよ。
答え（８√６π）/２７
半径が求められません。
解き方を教えてください。　
解説が詳しいとありがたいです。

回答No.4

info22_ · ベストアンサー

図のように記号と補助線を引く。
図の右側に
正８面体ABCDEFの内接球Ｏの半径Rと体積Vを求める
詳細な計算過程を書きました。

回答No.5

momordica

他の回答者の方々のおっしゃるように、この半径は適当に補助線を引いたりして
三平方の定理なり相似なり使えば簡単に求まるのですが、別の方法としては、

四面体の内接球の半径を求めたりするのに良く使われる方法ですが、
一般に、半径rの球に外接する（すべての面が球に接する）多面体の体積をV、
表面積をS、とすると
　V=r*S/3
となります。
四面体においてこれが成り立つ理由を考えてみればお分かりになると思いますが、
これは八面体でももちろん有効です。
したがって、今回の問題の場合、
　V=(8√2)/3
　S=8√3
ですから、これらを適用すれば
　r=(√6)/3
と求めることができます。

もし、正八面体の体積や表面積の求め方が分からないなら、またご質問ください。

回答No.3

ferien

一辺の長さが２の正八面体ABCDEFがある。この正八面体に内接する球の体積を求めよ。
答え（８√６π）/２７
＞半径が求められません。

正八面体のＡ－ＢＣＤＥの部分を考えます。
Ａから正方形ＢＣＤＥに垂線をおろして、交点をＨとすると、
Ｈは、正方形の対角線の交点で、内接球の中心でもある。
△ＡＢＣでＢＣの中点をＭとすると、△ＡＢＣは１辺２の正三角形だから、高さＡＭ＝ルート３
△ＨＢＣから、ＢＭ＝１，ＨＢ＝ルート２（ＨＢは正方形ＢＣＤＥの対角線の半分）より、
高さＨＭは、△ＨＢＭが１：１：ルート２の直角三角形だから、ＨＭ＝１

△ＡＭＨを考える。ＡＨは垂線だから直角三角形
ＨからＡＭに垂線を引いて、交点をＰとすると、ＨＰが内接球の半径になる。ＨＰ＝ｒとおく。
ＡＨ^2＝ＡＭ^2－ＨＭ^2＝（ルート３）^2ー1^2＝２より、ＡＨ＝ルート２
△ＡＭＨと△ＡＨＰは相似。（角Ａ共通、直角もあるから２つの角が等しいから）
よって、ＡＭ：ＡＨ＝ＨＭ：ＨＰより、ルート３：ルート２＝１：ｒ
よって、ｒ＝ルート６／３

内接する球の体積＝（４／３）×π×（ルート６／３）^3＝（８√６π）/２７

でどうでしょうか？図を描いて考えてみて下さい。

回答No.2

kaztel-D4C

方針として、正八面体の上半分（正四角錐）の体積を、球の半径の値で表現できるか考えます。
正八面体に内接している球の中心は、正四角錐の底面BCDEの対角線の交点上にあります。これをOとします。
すると、正八面体と球が接する接点と、点Oとの距離は球の半径と等しくなりますから、この半径をrとします。

今、面ABC上の、正八面体と球の接点をHとすると、線分OHは面ABCと垂直となります。つまり線分OHは、四面体OABCで底面を面ABCとした時の高さに相当します。
線分OHはrと等しいですから、四面体OABCの体積V1は、
V1＝２×√３×(1/2)×r×(1/3)です。
ここで、同様に四面体OACD、OAED、OABEを考えるとそれらの体積は全てV1と等しいです。
よって、正八面体の上半分（正四角錐）の体積Vは、
V＝V1×４＝2×√3×(1/2)×r×(1/3)×4=(4√3r)/3・・・(1)　です。
このrを出すために、正四角錐の体積Vを、より一般的な「底面積×高さ×1/3」の公式から求めます。

底面を面BCDEとした時、高さ（AO）は√2ですから、（三平方の定理BO^2+AO^2=AB^2から出ます）
V=2×2×√2×(1/3)=(4√2)/3・・・(2)　になります。

よって(1)と(2)からr=√6/3となるので、あとは球の体積の公式に当てはめれば答えが出ます。
わかりにくい文章かもしれませんが、以上で回答とさせていただきます。

回答No.1

Tacosan

座標は使っていい?