- ベストアンサー
寄棟屋根の「高さ」を「立面図」から算出する方法
寄棟屋根の「高さ」を「立面図」から算出する簡単な方法を教えてください。 「立面図」は、勾配の分、「高さ」が短くなっていますよね。 切妻屋根なら、隣合わさった立面図の「流れ」を測れば、わかるのですが・・ 知りたい目的は、屋根に何枚ソーラーパネルが載るのか 自分で調べたいからです。
- みんなの回答 (8)
- 専門家の回答
その他の回答 (7)
- shorun
- ベストアンサー率42% (133/310)
No4,5の回答者です。 No6さんの慎重なご指摘に目が覚めました。 私は、辺ACが必要だとの思い込みで回答して、No3を否定する内容であったことになり No3さんにお詫び申し上げます。 ところで No6のお礼に知りたいのは「辺ABなのでNo2の方の回答の通りにいたします」とありますが、 辺ABは寄棟の長さのことであり、立面図には表示されませんから No2の方法(No4,5も同じ)では辺ACは測れても、辺ABは測定不可能です。 辺ABは平面図には表示されますが、投影寸法で、屋根に登って測る実寸とは違います。 ●結論、辺ABを求めるなら No3お礼「これなら私にも納得できます!(喜)ピタゴラスの定理ですね」が正解です。 ◆老婆心 ソーラーパネルの枚数を検討するなら 辺ABよりACまたはADを優先して検討するのが妥当だと思います。 ABなのかACなのかよく考えて誤算のないようご留意ください。

お礼
shorunさんのおけげで、モヤモヤ感が解消されました。(感謝) 私は、ソーラーパネルの枚数を調べたい、それには 台形の屋根の「高さ」(辺AC)を求めることが必要だ それは、三角形の「立面図」の斜辺(辺AB)と同じである ということで、整理できました。(それで、合ってますよね?) shorunさんは ちゃんと、私の立場に立って教えてくださいました。 何がわからないのか、私以上に分析して教えてくださいました。 その誠実なご姿勢に、深く敬意をささげます。
- yotti0315
- ベストアンサー率46% (6/13)
屋根勾配(角度もしくは何寸なのか)と桁行・梁間方向(縦横)の長さが分かれば算出できますよ。 (1)各寸法の関係は図のとおりです。 寄棟屋根では屋根伏図上の隅(登)棟(斜めに走っている線)は必ず45°を通ります。 梁間の長さが分かれば、陸棟までの水平投影距離が算出できます。 ちなみに陸棟が全く無い屋根が方形屋根となります。 (2)屋根の投影(平面上の)面積S1’=A^2/4(小平の場合)となります。 (3)投影面積をcosτ(τは屋根勾配○○°)で割るか、{√(100+X^2)}/10(Xは屋根勾配○○寸)を掛ければ本当の屋根面積が算出できます。 ・屋根面積S1or2 = S1'or2'/cosτもしくはS1'or2'×{√(100+X^2)}/10 ・頂部(陸棟)高さt=(A/2)/cosτもしくは(A/2)×{√(100+X^2)}/10 投影面積と実際の屋根面積の関係は、0寸(フラット)は1倍、5寸は1.118倍、10寸(カナ勾配、45°)は1.414(√2)倍になります。

お礼
ありがとうございます。 この世界を、ちょこっと覗けた感じがします。 はぁ~っ!!って感じです。 ついていこうと調べてみましたが、 「梁」や「桁」の意味がなんとな~くわかったところで断念でした。 こういうことわかったら面白いだろうなぁ・・と思いました。 本当にありがとうございます!!
- shorun
- ベストアンサー率42% (133/310)
No2さんご回答のとおりです。 お知りになりたい屋根の斜面の長さは A です。 添付図の a を測ると高さで 、A を測れば斜面の長さです。

お礼
やはり図解は、わかりやすいですね。 ご親切に本当に感謝しています! たしかに、shorunさんやNo2さんが仰ることと同じことを 周りの人も教えてくれました。 「何を難しく考えてるの? いたってシンプルだよ。」って。 だけど、 >A を測れば斜面の長さです。 ここが、私にはわからないんです。(すみません) 本当にこれで納得できれば、とても簡単ですよね。 でも 三角形の面の立面図では、斜辺(隅棟?)が勾配しているため 短くなっていると思ってしまうんです。 (じっさいに、紙を切って測ってみたりしたんです) たとえば、切妻屋根の切り落とされた三角形の斜辺(ケラバ?) であれば、勾配がないので、 >A を測れば斜面の長さです。 ということが納得できるんです。 すみません。周りの人は「なんでわからないの?」といぶかしむので もう、これ以上「わからない」って言えなくて、困っています。 お願いですから、そこのところを教えてくださいませ。 モヤモヤしたままなんです。
- fujiyama32
- ベストアンサー率43% (2306/5313)
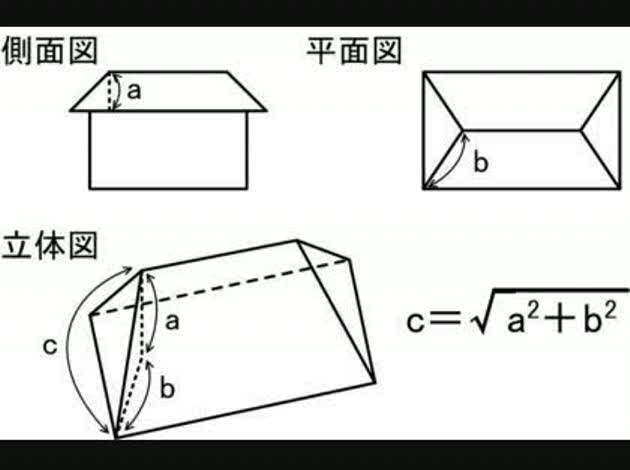
斜線(勾配面)の長さは、添付図を参照して下さい。 次の式から計算できると思います。 C=√(a^2+b^2) ただし、 a:側面図の高さ b:平面図の斜線部分の長さ c:立体図の斜線(勾配面)の長さ とします。

お礼
おおっ!!なんと! これなら私にも納得できます!(喜) ピタゴラスの定理ですね。 3D図面まで、ご用意いただいたおかげで 飲み込みの良くない私にも、理解できました。 ご親切な図解に大感謝です!!
- runksmoru
- ベストアンサー率66% (6/9)
こんにちは。 寄棟屋根を立面図で見ると、ある面が台形だとすれば、それと隣り合った面が三角形になってますよね。 三角形の斜辺に、定規を斜めなりに当てて測ると、棟から軒先までの長さということになります。 切妻屋根の、斜辺を測ることと同じです。

お礼
やさしく教えてくださり、感謝です! めちゃめちゃ わかりやすいです! >(隣り合った)三角形の斜辺に、定規を斜めなりに当てて測ると、 >棟から軒先までの長さということになります。 そこなんです! 台形の棟から軒先までの長さを知りたいときは 隣り合った三角形の斜辺を測ればいいのですね。 すごくわからずやで恐縮なんですが 寄棟なので、その三角形も勾配を持っていますよね。 とすると、その斜面も、立面図では、 実際の長さより短いのかなぁ・・?と思ってしまうのです。 真横から見た立面図の長さは、勾配があると短く見えますよね・・?
- tadagenji
- ベストアンサー率23% (508/2193)
建物の高さとは、地盤面から垂直に測ったものを言います。 立面図の高さは、屋根に勾配があろうとなかろうと高さは同じです。 あなたがおっしゃりたいのは、屋根面の長さのことでしょうか? それなら別の面の立面図で勾配面の長さが出ています。 確認申請には、立面図を2面付けますので図面上で判断できます。

お礼
さっそくのご回答、ありがとうございます! 私は、「高さ」の定義を間違えていました。 すっきりとご指摘いただき、感謝です。 >それなら別の面の立面図で勾配面の長さが出ています。 「勾配面の長さ」とは、「流れ」のことでしょうか? 質問者である私はシロウトです。 調べたばかりの言葉を使いながらの質問なので、 何を聞きたいのかわかりにくいかもしれませんが、 どうぞよろしくお願いします。






















お礼
shorunさん 単純明快にお答えいただき感謝です。 すっきり、この通り覚えます。 ご親切なご対応、本当にありがとうございました!!